Find the code for this post at https://github.com/jjhbw/hospital-schedule

Physician Scheduling

Shift scheduling of doctors in a hospital is a notoriously complex puzzle. This process is often a manual, time-consuming task that can take days of a planner’s time. Some departments even let the doctors do it themselves, and time spent creating shift schedules is time not spent on patient care.

As a typical software nerd, I couldn’t resist grossly underestimating this problem. We have solvers for this! Math! AI! How hard can it be?! Well, hard. As you can read in the rest of this post, I got pretty far, but it is nowhere near production-ready. It was a lot of fun to try, though! These kinds of optimization problems are incredibly satisfying to work on.

Can this be automated?

The goal of this project was to explore the feasibility of fully automating the shift scheduling process for a hospital. I wanted to see how far I could get in automating this complex process. The aim was to create an automatic scheduler that respects the myriad of constraints that govern a physician’s schedule.

The Challenges

Why is creating a shift schedule like this so hard to automate? Why is this seemingly menial task still done by hand today?

A Sea of Constraints

The complexity of physician scheduling stems from the sheer number of constraints that must be satisfied. These are not just simple rules; they are often interconnected, sometimes contradictory, and always important. I sat down with my doctor friend for an hour to try and find all constraints and rules involved. It seemed that every time we had one constraint written down and prioritized, she managed to think of another one. Note that we are only working on the physician shift schedule. Nursing staff is an entirely different story.

To preserve my sanity, I limited this project to what I thought were the 8 most important constraints. Coincidentally, these were also the 8 constraints I found to be the easiest to model. Weird how that happens.

National and personal holidays

The schedule must account for national holidays, during which staffing levels are different. More importantly, it must respect the personal vacation and off-day requests of each physician. This adds a layer of personalization that makes a generic solution impossible.

Part-time contracts and availability

Due to the intense nature of the work, many physicians work on part-time contracts and have one day off every week or every other week. In practice, this generally means they still work 40+ hours per week, but are unavailable on certain days. The schedule must respect these contracts, ensuring that physicians are not scheduled on their days off. Furthermore, individual physicians may have specific availability requests that need to be considered.

Understaffing

Perpetual understaffing is a harsh reality in many healthcare systems, forcing schedulers to make difficult trade-offs. When there aren’t enough physicians to cover all shifts optimally, the optimizer must weigh hard-to-quantify problems against each other. For example, is it better to have one physician work a double shift, or to have two physicians work on their day off or the day after a night shift? Even more dramatically, sometimes it is better to ‘close’ a shift simply because it cannot be covered. These are the kinds of questions that make scheduling a truly challenging optimization problem.

Dramatic employee churn

The average tenure of a non-resident doctor is about a year, because they job-hop a lot to broaden their expertise before starting a residency. This means you constantly have to take the start and end dates of someone’s employment into account. Not to mention the ramp-up time and expertise gaps that come with this.

Informal constraints

Some constraints are simply never formalized, and you only run into them once you have a draft schedule. “Hey, Dr. X has no experience running that shift, so he needs to be backed up by someone with experience!” You now need to schedule two doctors on one shift, just for a single instance. How are you going to encode this constraint in your model, without dramatically complicating it?

Implementation

Hard vs. soft constraints

In the world of optimization, constraints come in two flavors: hard and soft.

Hard constraints are the unbreakable rules of the system. The constraints that must be satisfied for a solution to be considered feasible. In our scheduling model, these include:

• One shift per day: An employee cannot be in two places at once.
• Shift clustering: To ensure continuity of care, a single employee is assigned to a shift for a minimum of 4 and a maximum of 6 consecutive days.
• Compensation days: After a block of night or evening shifts, an employee is guaranteed time off to recover.
• Weekend consistency: The same employee must work a shift on both Saturday and Sunday to ensure continuity of care.

Soft constraints, on the other hand, are more like strong suggestions. These are the “nice-to-haves” that the model tries to satisfy, but can violate if necessary, for a price. Each soft constraint has a penalty associated with it, and the solver’s goal is to find a schedule with the lowest total penalty. This is where the real magic happens, as the solver navigates the complex trade-offs between competing objectives. Our soft constraints include:

• Covering every shift: While the goal is to have every shift covered, sometimes it’s better to leave a shift uncovered than to, for example, ask staff to work overtime in unsustainable ways. Penalty: the penalty can be configured per shift type (defined in shifts.csv), typically 100 points per uncovered shift.

• Limiting undesirable shifts: To prevent burnout and other health issues associated with night shifts, the model tries to limit the number of night, evening, and weekend shifts per employee. Penalty: 10 points per excess undesirable shift beyond the soft limit of 12 per 90-day period (scaled proportionally for shorter scheduling periods).

• Shift clustering: Shifts should be assigned in sequential blocks to ensure continuity of care, with sequences ideally lasting 4-6 days. Penalty: 20 points per day for sequences exceeding 5 consecutive days (sequences shorter than 4 days are forbidden as hard constraints).

• Granting time-off requests: The model is incentivized to approve time-off requests, but can deny them if the cost to the overall schedule is too high. Penalty: Variable per request (defined in requests.csv), representing the importance/urgency of each specific request.

• Balancing workload: The model aims to distribute the total number of shifts as evenly as possible among all employees. Penalty: 1 point per shift deviation from the expected average workload per employee.

The weights of the different penalties are based on intuition and aim to strike a balance between these sometimes conflicting objectives. Each penalty’s weight determines how the solver balances competing objectives. Should it prioritize covering all shifts, or is it more important to respect vacation requests? How much worse is leaving a shift uncovered compared to forcing someone to work overtime?

For example, denying a vacation request has a penalty of 100, while leaving certain shifts uncovered also carries a penalty of 100. An employee working excessive undesirable shifts (nights, evenings, weekends) incurs a penalty of 10 per excess shift. In a production scheduling system, these weights would ideally be calibrated through collaboration with actual schedulers and doctors.

As this project was just a weekend hack, I completely made up the penalty weights you see in the input data CSV files. I used educated guesswork and vibes.

Employee time off requests

One of the most important features of the scheduling system is its ability to handle employee requests for time off or specific shift preferences. The system supports four types of requests: complete days off (off), avoiding night shifts (no_night), avoiding evening shifts (no_evening), or avoiding both evening and night shifts (no_evening_or_night). Each request specifies an employee, a date range, the type of request, and crucially, a penalty value that represents the cost of denying the request.

The request system operates as a soft constraint within the optimization framework. When processing a request, the solver identifies all relevant shift assignments that would violate the request within the specified date range. It then creates a “request denied” boolean variable that becomes true if any conflicting assignments are made. The penalty associated with denying the request is added to the objective function, meaning the solver is incentivized to grant requests but can choose to deny them if doing so significantly improves the overall schedule quality.

This approach provides flexibility in handling competing priorities. High-priority requests (such as medical appointments or family emergencies) can be given higher penalty values, making them more likely to be granted, while routine requests with lower penalties might be denied if necessary to maintain adequate staffing levels. The system effectively automates the complex decision-making process that human schedulers face when balancing individual preferences against operational requirements.

Realistic input data

To truly understand how well your model is performing, realistic input data is essential. If your input data is unrealistic, it is easy to create a solution that appears optimal but falters when deployed to production. Operations research projects are similar to machine learning projects in that regard.

To get some realistic data, I asked my doctor friend to help build a realistic dataset of shifts, vacation requests, and employee availability. For this, we used one of his department’s old shift schedules from 2022.

This dataset, based on real-life data, includes three core shift types: day, evening, and night. These can be assigned to run on weekdays, weekends, or holidays, as defined in the shifts.csv input file. The number of available employees is also configurable through a separate employees.csv file. The current implementation plans approximately five months ahead, from January 1st to June 3rd, 2022, which is typical for these types of shift schedules.

Google’s OR-Tools and CP-SAT

To solve this optimization problem, I turned to Google’s OR-Tools, a suite of open-source software for combinatorial optimization. OR-Tools is an absolutely amazing tool, providing a unified interface to a variety of solvers, including Google’s own CP-SAT solver.

The CP-SAT solver is a constraint programming solver that uses satisfiability (SAT) methods. It is very flexible, allowing you to express almost any imaginable constraint. This was crucial for this project, as it allowed me to model the complex rules and constraints I needed. The ability to define ‘soft’ constraints with integer penalties was essential for navigating the trade-offs caused by understaffing.

One of the most sophisticated constraints in this model demonstrates the flexibility of constraint programming with CP-SAT. Consider the requirement that shifts must be assigned in sequential clusters of 4-6 consecutive days. This isn’t just “assign at least 4 days”, it means “prevent any isolated sequences shorter than 4 days while penalizing sequences longer than 5 days.”

To implement this, the solver uses a function called negated_bounded_span. For every possible short sequence (say, 3 consecutive days), it creates a constraint that says: “Either this sequence is NOT all assigned to the same person, OR the days immediately before or after are also assigned to that person.” This clause prevents isolated short sequences while allowing longer valid ones.

This type of complex logical constraint would be extremely difficult to express in traditional mathematical programming approaches, but constraint programming handles it naturally. It’s this expressiveness that makes CP-SAT shine in real-world scheduling problems.

Solving in the Cloud: Google Cloud Batch

Solving a large-scale scheduling problem can be computationally intensive. To avoid tying up my local machine for hours, I wanted to try offloading it to the cloud. Google Cloud Batch seemed like a good fit for this. I could simply package my solver as a Docker container, push it to the GCE container registry, and then submit it to Cloud Batch using the gcloud CLI tool.

I’m not a huge fan of the API, but once you get all the permissions and magic API incantations figured out, it is pretty satisfying to see Cloud Batch automatically schedule jobs on cheap spot instances and decommission them automatically afterwards. I also tried AWS Batch, but found the interface completely baffling.

At runtime, the solver writes all feasible solutions it finds to CSV files. Mounting a Google Cloud Storage bucket as a filesystem to the container allows you to reliably write these files to persistent storage.

I don’t want to turn this post into a ‘How to Configure Google Cloud’ thing (booooring), but I added some rudimentary instructions on how to set this up to the GitHub repo.

Visualizing the solver outputs

A schedule is much easier to understand when visualized. Because the solver needs to balance multiple conflicting objectives, visualizing the solution helps in understanding the trade-offs made in each solution. The solver script writes all feasible solutions to numbered files, which can then be visualized.

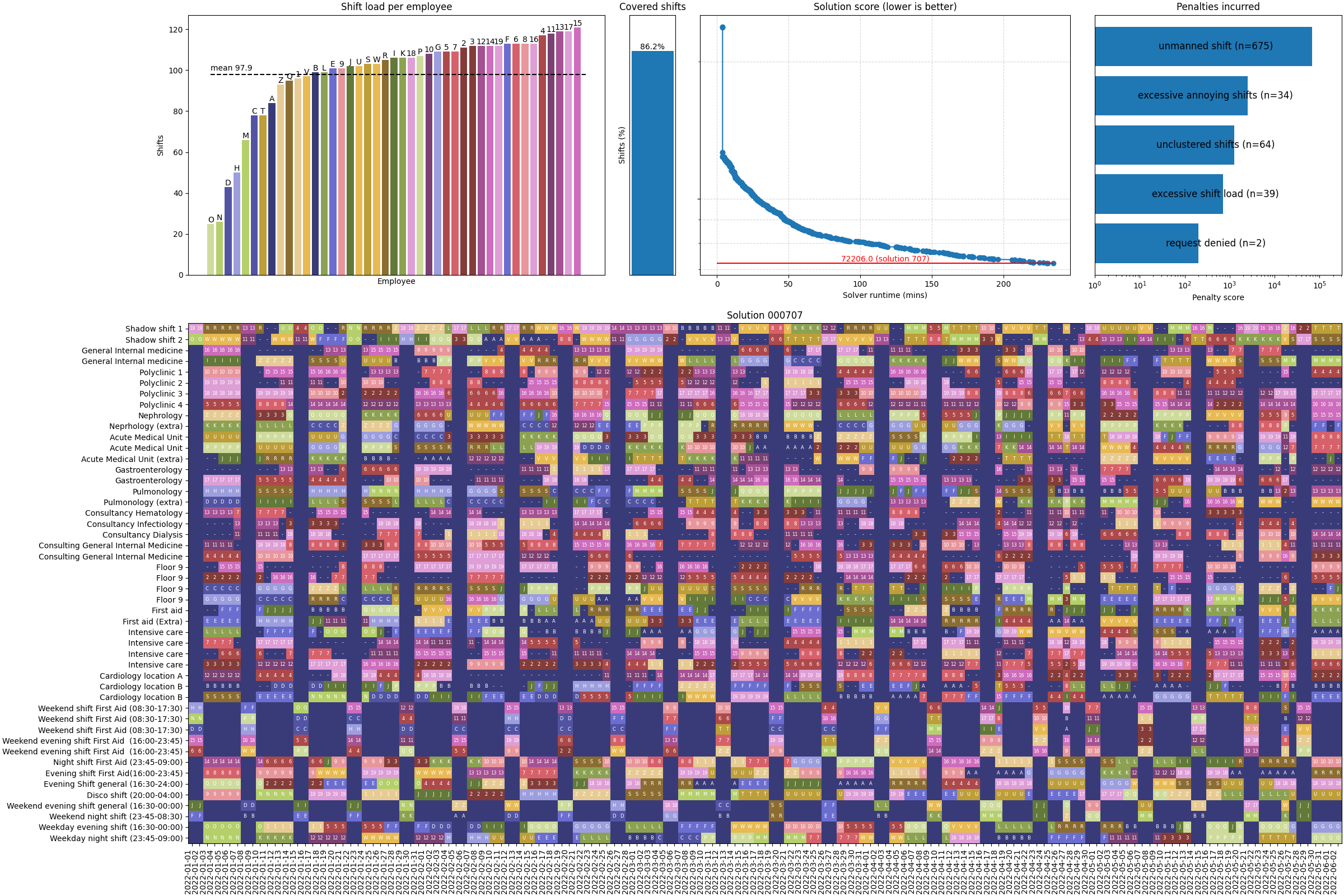
Below is an example of a (very bad) solution to this scheduling problem.

In the above example, all shift types are listed on the Y-axis, and all dates on the X-axis.

• Every cell in this matrix represents a shift.
• Dark purple cells represent uncovered shifts, and colored cells are covered shifts.
• Some shifts are always uncovered, for example, because that department is closed during the weekend.
• Shifts that are uncovered but ideally should be covered contain a white dash (-).
• The letter or number is the doctor’s identifier (numbers for residents, letters for non-residents).

Results

Experiment 1: Dangerously Understaffed

The first experiment features a scenario with significant understaffing. There are simply not enough doctors available, so the solver must make immediate trade-offs. We have 19 residents and 24 non-residents. I ran the solver on a 16 vCPUs, 32GB memory GCP spot instance with a time limit of 4 hours.

The solver in action

As you can tell from the video, the solver struggles to find improvements after a while and has to leave about 14% of shifts unmanned even after 4 hours of solving! The schedule looks like Swiss cheese. I wouldn’t want to be a patient in this theoretical hospital… Still, this result may be close to the optimal solution given the available staff.

Best result of experiment 1

Experiment 2: Throw Some Residents at the Problem

Let’s add some personnel to alleviate the understaffing problem. Determining optimal staffing levels is a hard problem on itself, but let’s go big and add 8 residents who work 5 days per week. These 8 doctors are absolute machines: they are qualified to work any shift and don’t take days off (except weekends). Adding new employees grows the model, so a c2d-highcpu-32 instance with 64GB memory was necessary to run the solver.

Because these instances also come with double the vCPU, the solver found significantly more solutions within the allotted 4-hour timeframe.

Before presolving the model contains:

Variables: 427'317 (#bools: 243'865 #ints: 102 in floating point objective) (413'303 primary variables)
- 427'163 Booleans in [0,1]
- 51 in [0,20]
- 102 in [0,153]
- 1 constants in {0}
kAtMostOne: 7'803 (#literals: 374'544)
kBoolAnd: 42'942 (#enforced: 42'942) (#literals: 4'036'344)
kBoolOr: 1'210'800 (#literals: 6'722'304)
kExactlyOne: 4'886 (#literals: 251'890)
kLinMax: 102 (#expressions: 204)
kLinear0: 873
kLinear2: 9'225
kLinear3: 1
kLinearN: 59 (#terms: 184'099)

The solver in action

The best solution

As you can see, the solver managed to assign 99% of shifts! Pretty good for a 5-month schedule. In the top-right figure, you can see which compromises it had to make to get to this solution. Let’s take a look at the penalties that were incurred:

• 48 shifts are uncovered: given that this is a 5-month schedule, this is likely a manageable number that human schedulers can address manually. If not, we can increase the penalty for uncovered shifts on a shift-by-shift basis and rerun the solver.
• 77 ‘unclustered shifts’: continuity of care had to be broken 77 times more than the theoretical optimum. This is inevitable in a complex schedule when not massively overstaffed. Only a medical professional can evaluate whether this number is acceptable. Some sub-departments or shifts may be more sensitive to doctor changes than others.
• 21 instances of ‘excessive undesirable shifts’ means the heuristically expected number of night/evening/weekend/holiday shifts was exceeded 21 times. It does not specify which doctor is most affected by this, which is a limitation of the current implementation.
• 41 instances of ‘excessive shift load’: 41 shifts were assigned to doctors who already had an above-average workload. The ‘shift load per employee’ figure shows that this penalty is highly dependent on the distribution of shift assignments. This heuristic is also biased by doctors who work part-time. More doctors working part-time means a lower mean workload per employee, causing this penalty to trigger more often for the full-time working staff. There is room for improvement in the model design here.
• The solver accepted all vacation and time-off requests! Very good for morale. Though in this example data, there weren’t that many requests to begin with, so this was probably an easy win for the solver.

Conclusion

That was fun! It is extremely satisfying to see a solver like this working. Each time I added a constraint to the model, I wondered whether the solver would break or stall. But it didn’t! CP-SAT and OR-Tools are really impressive pieces of software. I was very surprised that a complex schedule like this, with all its constraints and its huge number of interacting variables, can be solved within a tractable timeframe. There are likely many aspects I could have modeled better, but the classic solution of throwing a lot of compute at a problem got me very far.

Ideas for future improvements:

• Schedules rarely exist in isolation. It would be cool if we could start the solver from an existing static schedule. This would enable it to take into account a doctor’s shift load in the previous time period, for example.
• Variable ‘excessive undesirable shift’ penalties per doctor. Some doctors may prefer overtime pay, while others may find night shifts more burdensome due to e.g. pregnancy or childcare.
• Try a different solver. I have read good things about HiGHS. I am not sure how easy it is to transfer the model definition to this solver, but it looks like it would be fun to try.